MarvelCode

Paper link : https://tapvid.github.io/

➡️ Abstract

Computer Vision 분야에서 영상 데이터의 motion을 해석하는 방식에는 물체 추적(Tracking objects)과 표면의 변화 및 이동 인식(Perceiving surface deform & move)이 있다. 이러한 정보는 물체의 3차원 형태나 물리적인 특성, 상호작용을 이해하는데 사용될 수 있다. 하지만 길이가 긴 영상 데이터에서 멋대로 변화하는 표면 위의 지점(physical points on surfaces)을 추적하는 task는 성능 평가를 데이터셋이나 benchmark가 존재하지 않는다는 문제가 있다. 본 논문에서는 처음으로 Tracking Any Point (TAP) 문제를 정의하고 이를 평가할 수 있는 benchmark인 TAP-Vid를 소개한다. 또한 이를 benchmark를 통해 학습된 TAP end-to-end 모델인 TAP-Net을 소개한다.

➡️Introduction

Motion을 인식하는 것은 비전 분야에서 세상을 이해하는데 중요한 tak이고 그 동안 많은 연구가 이뤄져 왔지만, 장기간의 영상 데이터의 point 변화를 추적하는 task는 그렇지 못했다. 이뤄졌던 여러 종류의 연구들도 아래와 같은 명확한 단점들이 있었다.

• Box & Segment tracking
  • 표면의 deformation과 rotation을 고려하지 못함
• Optical Flow
  • 오직 두 frame 쌍 사이의 point track만 수행할 수 있음
  • 가려짐(Occlusion)을 고려하지 못함 
• Keypoint matching
  • 특정하게 관심있는 포인트(e.g. 관절)에 대해서만 tracking 수행
  • 물체의 변형이나 뚜렷하지 않은 질감에 대해 고려하지 못함

본 논문에서는 Tracking Any Point (TAP) 로 명명한, 길이가 긴 영상 데이터에서 물리적인 point를 추적하는 문제를 정의한다. 저자가 제시하는 방법론은 오직 하나의 \(\textit{query}\) 픽셀만 입력으로 받으면, 해당 target point가 속해 있는 표면을 결정하고 영상 데이터에서 시간에 따른 움직임을 예측할 수 있다 (단, 투명한 물체, 액체, 유리는 다루지 않음). 해당 방법론의 학습과 평가는 실제 영상 데이터(real world) 와 생성한 영상 데이터(synthetic)를 섞어서 사용했는데, 이때 사용하는 실제 영상 데이터에서 ground truth를 사람이 수동으로 표기하는 것은 쉽지 않은 방식이다. 따라서 저자는 실제 영상 데이터에서 효과적이고 정확하게 point track을 표기(annotation)하는 pipeline을 개발했다. 이를 통해 1,189개의 Youtube 영상을 각각 약 25개 이상의 points로 labeling 했다. 이후에는 소수의 Annotator를 통해 label을 검증하는 과정을 거쳤다.

해당 논문에서 주장하는 3가지 Contribution은 아래와 같다.

1. Annotator(실제 영상 데이터의 point를 labeling하는 사람)가 더욱 정확하게 작업하도록 도울 수 있는 알고리즘을 개발하고 평가했음
2. 총 1,219개의 평가용 실제 영상데이터(총 31,951개의 points)를 만들었음
3. 기존의 사람 key point tracking 데이터 셋인 JHMDB와 논문에서 제시한 TAP-Vid 데이터셋을 각종 baseline 알고리즘들을 통해 비교한 결과, TAP-Vid 데이터셋이 학습에 더 용이하다는 결과를 얻음

➡️ Related Work

(중략)

➡️ Dataset Overview

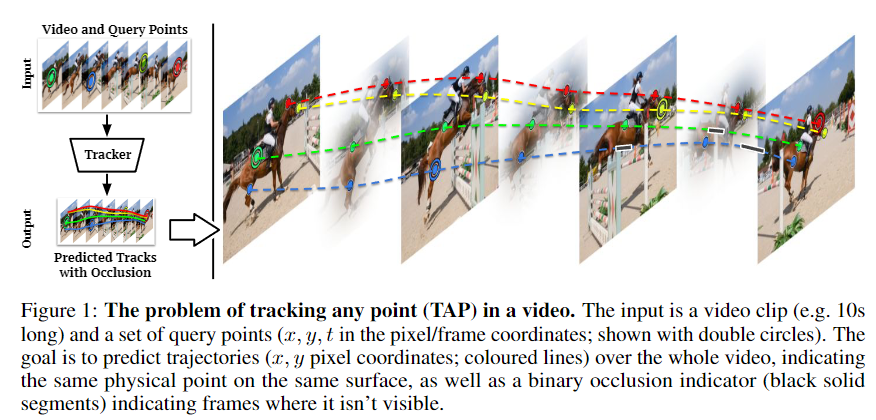
본 논문에서 제시한 방법론은 입력으로 영상 데이터와 \(\textit{query}\) points \((x, y, t)\)를 전달 받는다( \( {x, y} \) 는 2차원 위치, \( {t} \) 는 시간 ). 그리고는 각 query point 마다 1) 모든 frame별로 point가 움직인 위치 \((x_t, y_t)\)와 , 2) point가 모든 frame별로 가려졌는지에 대한 여부 \({o}_t\) 를 산출해야한다. 단, point가 가려져있는(occluded) 동안에 예측되는 \((x_t, y_t)\)는 무의미한 값이다. 

저자는 TAP 분야의 평가를 위한 benchmark를 만들고자 하는 목적으로 실제 영상 데이터와 생성된 영상 데이터를 섞은 TAP-Vid를 만들었다. Kubric과 같이 특정 생성된 데이터를 포함하는 세트를 평가 데이터로 사용하는 것은 특정 도메인에만 편향된 학습 결과를 보여줄 수 있기 때문에, 저자는 학습에 Kubric 데이터만 사용하고 추가로 3가지 종류의 데이터를 더 만들어서 테스트에 함께 사용했다. 아래는 총 4가지 종류의 TAP-Vid 데이터에 대한 정보를 기술한 표이다.

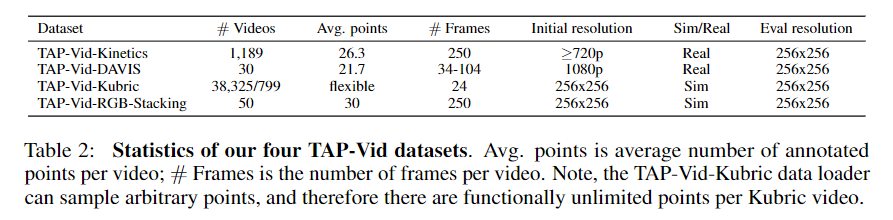
✔️ TAP-Vid Datasets

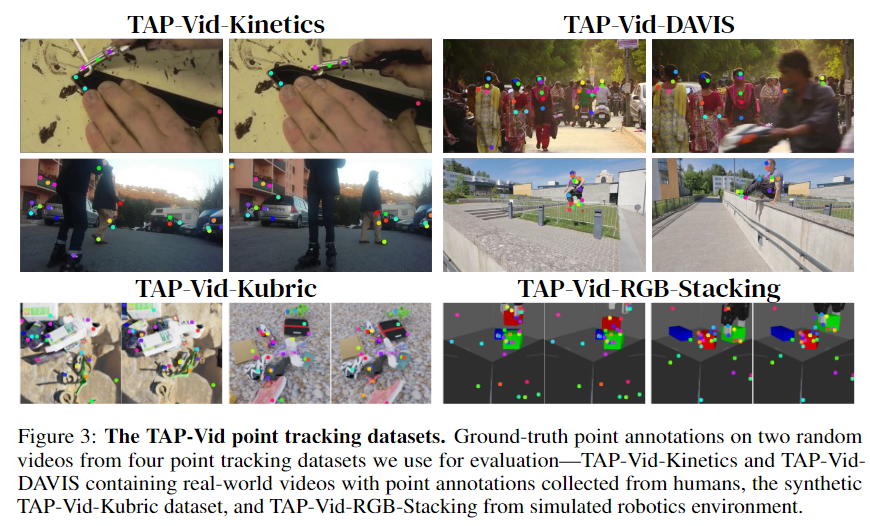
◾ TAP-Vid-Kinetics

• Kinetics-700 validation set에서 추출
  • 다양한 사람의 행동으로 구성된 데이터 셋 
  • YouTube에 업로드 되어있음
  • 720P 해상도를 가짐
  • 움직이는 물체가 여러 개라던지, 카메라가 흔들리고, 불필요한 밝기 변경되는 등 구조화되지 않은 데이터임
• 25 fps를 갖는 10초 단위의 clip으로 편집하여, 한 clip은 총 250개의 frame을 가짐

◾ TAP-Vid-DAVIS

• DAVIS 2017 validation set에서 추출
  • segment tracking을 위한 30개의 영상으로 구성됨
  • 1080P 해상도를 가짐
  • 레이블이 1개의 움직이는 물체에만 매겨져 있음
• Annotator를 통해서, 5개의 다른 물체에 5개의 다른 point를 레이블링함
• 256 x 256 크기로 편집함

◾ TAP-Vid-Kubric

• 본 논문에서 제시하는 모델 TAP-Net의 지도학습과 평가에 모두 사용된 데이터 셋
• Kubric에서 소개된 생성된(synthetic) MOVi-E dataset에서 추출
  • 각 영상은 Bullet의 물리 엔진과 Blender의 레이트레이싱이 적용된 약 20개의 사물들로 구성됨
• 모델 학습을 위해서 augmentation을 적용함, 최대로 2:1 화면비, 최소로 픽셀 수 30%로 cropping

◾ TAP-Vid-RGB-Stacking

• 생성된(synthetic)데이터로, robotic stacking 시뮬레이터를 녹화한 데이터 셋
  • 원격 조종자가 다양한 기하학적인 모형을 원하는 대로 움직일 수 있는 시뮬레이터
  • \(\textit{triplet-4}\)라는 모형을 사용했고, 좌측 전면 카메라를 통해 녹화함
• 50개의 episodes를 녹화했고, 각 영상마다 30개의 points를 선택함 (20개는 움직이는 모형, 10개는 정적인 모형)
• 해당 데이터셋의 사물들은 질감이 없고(textureless), 회전축에 대해서 대칭(rotaionally symmetric)이며, 수시로 가려지기(frequent occlusions) 때문에 특히 더 어려운 데이터 셋임

➡️ Real-World Dataset Construction

Tracking Any Object (TAO)에 영감을 받아서, 논문의 저자도 annotator들에게 point 추적을 라벨링 할 위치를 지정해주기 보다는 일반화를 위해서 annotator이 원하는 물체 위의 원하는 임의의 point를 직접 선택해서 라벨링하게 했다. Annotator들은 총 15명으로 진행되었는데, 이들은 Google의 crowdsourcing pool에서 구인되었다고 하며 시급을 받고 진행했다고 한다. 저자는 소수의 annotator를 운용함으로써 작업자들의 전문성을 높혀 더 효과적으로 진행할 수 있었다고 한다. 아래의 그림과 같이 Annotation은 총 3단계로 이루어졌다. ( 각 단계의 자세한 내용은 아래에 기술 )

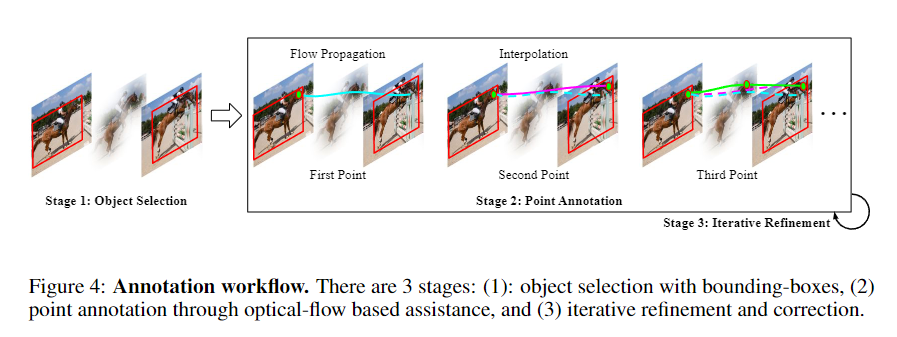
Stage 1: Object Selection

• 작업자는 \({K}\)개의 물체 수를 선택한다 (Kinetics에서는 \({K}=10\), DAVIS에서는 \({K}=5\) 사용)
• 눈에 띄고 오래동안 화면에 등장하는 순으로 물체들의 순위를 매긴다
• 30 frame에 한번씩 모든 물체에 대해서 box를 그린다
• 각 물체에 대한 텍스트 레이블을 작성한다

Stage 2: Point Annotation

• Stage1에서 선택한 모든 물체에 대해서, point 수 \({M}\)를 선택한다 (Kinetics에서는 \({M}=3\), DAVIS에서는 \({M}=5\) 사용)
• 작업자는 모든 frame에 대해 각 물체가의 위치가 변화할 때 동일한 point를 표시해야 하는데, 이때 optical flow를 활용한 \(\textit{track assist}\) 알고리즘을 통해 point의 움직임을 예측해서 작업을 도와준다
  
  • 단, 몇개의 sparse한 point는 작업자가 찍어줘야 한다
  • 해당 알고리즘에 대한 자세한 설명은 바로 다음 섹션에서 계속

Stage 3: Iterative Refinement

• Annotation 퀄리티를 확보하기 위해서, 최초 작업이 끝난 이후 결과는 두 번째 작업자에게 넘겨져서 작업이 잘 되었는지 확인한다
• 이 과정은 마지막 작업자가 모든 label에 대해서 승인할 때 까지 반복된다
• 평균적으로 4~5명의 작업자 기준, 10초짜리 영상의 작업은 3.3시간이 걸렸다

✔️ Track Assist Algorithm

Annotator에 의해서 첫 번째 point가 주어지게되면, RAFT와 같은 Optical flow 알고리즘을 통해서 이후 frame에서 해당 point가 어디로 움직일지 어느정도 예측이 가능하다. 하지만 이러한 방식에는 아래와 같이 두가지 문제가 있다.

1. 현재 point 이후 너무 많은 frame 뒤를 예측하게 하면, drift가 생겨 제대로된 예측을 할 수 없음
2. Occlusion을 고려하지 못함

두 번째 문제를 예방하기 위해 작업자들은 occlusion이 발생하면 작업을 멈추도록 교육을 받았고, 첫 번째 문제인 drift를 해결하기 위해서 Optical flow를 예측하는 알고리즘에 수정이 필요했다. 저자는 우선 RAFT를 이용해 전체 영상에 대해서 optical flow를 계산했고, 작업자가 frame \({s}\)에 대해 point \({p}_s\)를 선택하게 되면 미리 계산해둔 flow값과 선택된 point를 통해 마지막 frame까지 bilinear interpolation 사용해서 다음 frame point 값을 연산해서 넘겨준다. 작업자가 그 다음 frame \({t}\)의 point \({p}_t\)를 선택하게 되면, 각 frame 별로 optical flow 계산과 찾을 경로의 차이 제곱 값이 최소화 되게 하는 경로를 찾게 된다. 이를 식으로 표현하면 아래와 같다.

$  \operatorname{arg\,min}_{\rho\in{\mathcal{P}}_{s:t}}\sum_{i=s}^{t-1}\|(\rho_{i+1}-\rho_{i})-{\mathcal{F}}(p_{i})\|^{2}\qquad{\mathrm{s.t.}}\quad\rho_{s}=p_{s},\rho_{t}=p_{t} \tag{1} $ 

\( \mathcal{P}_{s:t} \)는 frame \({s}\)에서부터 frame\({t}\)까지의 모든 경로의 집합이다 (각 경로는 points들의 list). 따라서  모든 \({\rho}\)는 \( \mathcal{P}_{s \colon t} \) 에 속한다 ( \(\{\rho_i, i \in \{s, \ldots, t\}  \}\), \(where, {\rho}_i \in \mathbb{Z}^2\) ). 또한 \( \mathcal{F} \colon \mathbb{Z}^2 \rightarrow \mathbb{R}^2  \) 는 optical flow tensor를 뜻하고, 이 값에 의해 이미지 픽셀들이 optical flow vector로 매핑된다.

위 식은 non-convex 최적화 문제이지만, 각 프레임의 픽셀을 노드로 보면 그래프에서의 최단거리 문제로 간주할 수 있다. Frame \({i}\)에서의 각 픽셀은 frame \({i+1}\)의 모든 픽셀과 연결되어있고, 이때 각 연결의 가중치는 optical flow를 통해 게산한 두 경로 거리 차이의 제곱의 비율이다. 이는 곧 다익스트라 알고리즘을 통해 효과적으로 최단거리를 구할 수 있게된다. 이러한 알고리즘을 통해 annotator의 작업을 어느정도 도울 수 있게 된다.

✔️ Evaluation and Metrics

저자는 보이는 부분에 대한 정확한 point 위치 예측과 보이지 않는 point를 예측하는 것을 간단하게 표현할 수 있는 metric을 사용했다. occlusion 여부와 같은 binary decision과 위치 예측 regression prediction을 동시에 비교하는 것은 쉽지 않은 접근이기 때문에, regression 값에 treshold를 사용해서 binary 문제로 바꾸어서 아래의 3가지 Jaccard 스타일 metric을 산출한다.

1. Occlusion Accuracy \({OA}\)
   1. 가려짐 여부에 대한 단순한 classification accuracy 계산
2. \({\delta}^x\)
   1. 가려지지 않은 frame에서, 해당 threshold를 통해 position accuracy를 계산
   2. ground truth와의 거리가 theshold 보다 작은 포인트들의 비율을 계산
   3. 5가지 threshold 값을 변경하면서 결과를 평균내어 \({\delta}_{avg^x}\)를 계산 (각각 1, 2, 4, 8, 16 픽셀)
3. \(\text{Jaccard at }{\delta}\)
   
   1. 가려짐 여부와 position 위치 정확도를 동시에 평가
   2. \(\text{Jaccard} = \frac{True Positives}{True Positives + False Positives + False Negatives}\)
   3. \(\text{Average Jaccard (AJ)}\)는 \({\delta}_{avg^x}\) 에서와 같은 threshold를 사용한 결과의 평균

➡️ Datset Analysis

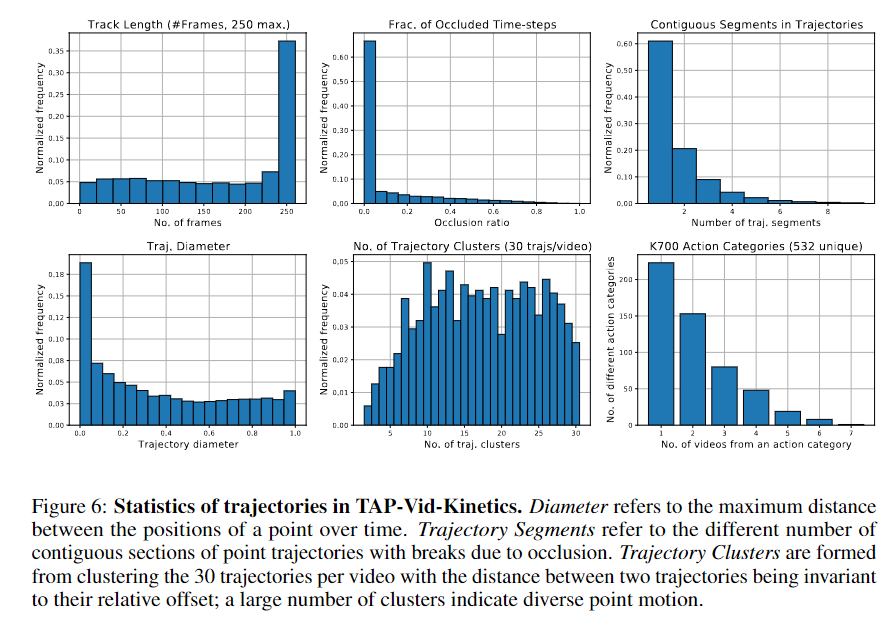
저자는 기본적인 데이터셋에 대한 통계치를 제공하고, 수동으로 annotating한 track에 대해 ground truth와 비교해서 point tracking에 대한 정확도를 평가했다. 또한 미래의 연구를 위해서 여러 방법론들에 대해 각 논문에서 제시한 알고리즘에 따라 baseline 성능 평가를 진행했다. 해당 알고리즘들의 성능이 우수하지 못해서, 저자는 cost volume을 활용해 좋은 성능을 확보한 TAP-Net baseline을 개발했다. 

➡️ Baselines

기존의 몇몇 방법론(e.g. Kubric-VFS-Like, RAFT, COTR)은 조금의 수정이나 확장을 통해서 곧바로 적용해 볼 수 있었다. 하지만 대부분 좋은 성능을 확보하지 못했다. 예를 들면 Occlusion을 고려하지 못하는 RAFT, deformable한 사물을 잘 다루지 못하는 COTR, 생성한 데이터에서 실제 데이터로 전이가 잘 이뤄지지 않은 Kubric-VFS-Like가 있다. 이러한 단점들은 모델의 구조적인 한계에서 비롯되기 때문에 저자는 이를 고려해 합리적인 성능과 빠른 실행시간을 확보한 딥러닝 구조를 개발했다.

✔️ TAP-Net

영상 데이터의 dense feature grid를 계산하고, query point와 다른 모든 point 사이의 feature들을 비교한다. 비교한 결과 값을 신경망구조에 입력해서 point 위치 값을 예측하고 occlusion 여부를 분류한다.

◾Cost Volume

저자는 optical flow 분야에서 성공적으로 사용되었던 cost volume에 영감을 받아 이를 응용했다. 먼저, 영상 데이터의 dense feature grid를 계산하고 query point와 다른 point의 feature들을 비교한다. 그리고서 비교한 쌍들의 집합 자체를 새로운 feature로 여겨서(cost volume), 이후에 신경망의 입력으로 사용한다. 이는 아래 Figure 7에 묘사되어 있다.

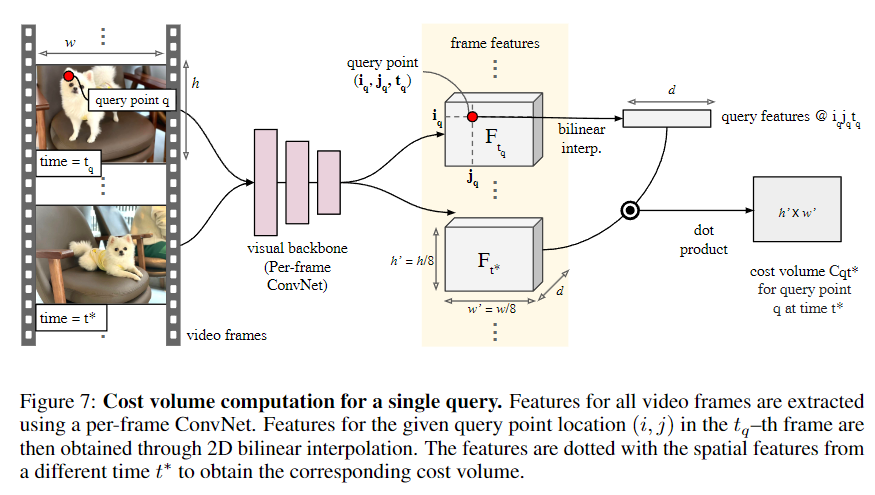
주어진 영상 데이터에 대해서 먼저 grid \({F}\)를 계산한다. \({F}_{ijt}\)는 시간 \({t}\)에서 좌표 \(i, j\)의 \({d}-\)차원 feature를 의미한다. 이를 위해 저자는 Per-frame ConvNet을 사용했는데, TSM-ResNet-18의 앞쪽 두 layer에만 time shifting을 적용해서 이를 구현한 결과는 좋지 않았기 때문이다. 시간 \({t}_q\) 의 query point 좌표 \({x}_q, {y}_q\) 가 주어졌을 때, feature grid \({F}_t\) 위의 \({i}_q, j_q, t_q\)에 대해 bilinear interpolation 해서 feature를 뽑는다. 이렇게 뽑힌 feature를 grid \({F}_q\)라고 칭한다. 그리고 행렬 곱을 통해 cost volume을 계산하는데, 즉 feature map \({F}\)위의 각 feature가 shape \({d}\) 을 갖는다면 출력값은 cost volume \({C}_{qijt} = F_q^{\intercal}F_{ijt}\) 이다. 따라서 \({C}_q\)는 3차원 tensor 이며, ReLU 활성화 함수화 함께 사용된다.

◾Track Prediction

다음 단계는 각 frame 마다 독립적으로 query point와 관련된 cost volume을 후처리하는 과정이다. 한 frame에 대한 처리 과정의 모식도는 아래 Figure 8과 같다.

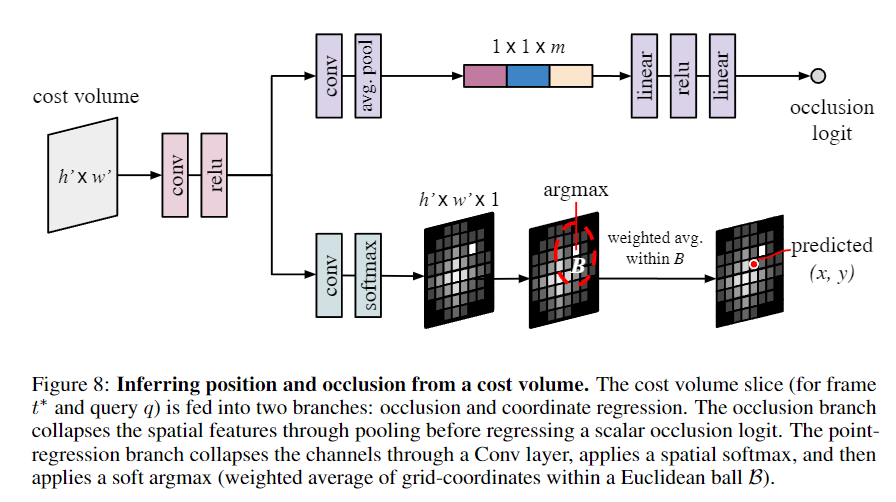
하나의 출력값을 갖는 Conv layer와 softmax를 통해 position 예측을 한다. 그 후 soft argmax와 spatial average를 취하는데, 이는 출력값 heatmap에서 가장 큰 값을 갖는 위치의 주변부를 활성화시키는 역할을 한다.

수학적으로 기술해보자면, query \({q}\)의 시간 \({t}\)의 공간 좌표 \({i}, {j}\)에 대한 softmax 활성화함수는 \({S}_{qijt} \in \mathbb{R}\)이라고 정의한다. 또 \({G}\)는 spatial grid라고 하자. 즉, \({G}_{i,j} \in \mathbb{R}^2\)는 \({S}_{i,j}\)의 이미지 좌표 공간에서의 위치이다. 마지막으로 \({S}_{qt}\)의 argmax 위치를 \((\hat{i}_{qt}, \hat{j}_{qt})\)라고 하면, 출력물은 아래와 같은 식으로 표현할 수 있다.

$ p_{q t}=\frac{ \sum_{i, j} \unicode{x1D7D9} \left(  \left\|  (\hat{i}_{qt}, \hat{j}_{qt} ) - (i,j) \right\|_2 < \tau \right) S_{qijt}G_{ij}}{\sum_{i, j} \unicode{x1D7D9} \left(  \left\|  (\hat{i}_{qt}, \hat{j}_{qt} ) - (i,j) \right\|_2 < \tau \right) S_{qijt}} \tag{2} $

위 식에서 \({\tau}\)는 상수이며, 보통 5로 사용했다. 해당 식의 일부분(thresholding과 argmax 부분)은 미분이 가능하지 않음에 주의해야한다.

◾Loss Definition

각 query point에 대한 loss는 아래와 같다.

$ {\cal L}(\hat{p},\delta,p^{g t},o^{g t})=\sum_{t}(1-o_{t}^{g t}){L}_{H}(\hat{p}_{t},p_{t}^{g t})-\lambda\left[\log(\hat{o})o^{g t}+\log(1-\hat{o})(1-o^{g t})\right] \tag{3} $

여기서 \(L_{H}\)는 Huber loss이고, \(p_{gt}\)는 위치의 ground-truth값, \(o_{gt}\)는 가려짐에 대한 binary ground-truth값이다. 즉 저자는 가려지지 않은 point에 대한 위치 예측을 단순히 frame별 regression 문제로 접근했다. error가 매우 커지는 만약의 경우를 대비해서 Hubber loss를 썼고 occlusion에 대해서는 binary cross entropy를 사용했다;

⚠️ 온전한 이해를 위해서 TAP-Vid 및 PIPs 논문 리뷰 선행 권장

Paper link: https://deepmind-tapir.github.io/

➡️ Abstract

본 논문에서는 영상데이터의 어떤 표면(surface)이나 지점(point)을 입력으로 받았을 때 효율적으로 trajectory를 추적할 수 있는 Tracking Any Point (이하 TAP) 모델 TAPIR(TAP with per-frame Initialization and temporal Refinement)을 제안한다. 해당 모델은 모든 frame에서 trajectory 예측의 후보군을 찾는 "matching stage"와 주변 feature을 사용해 trajectory와 query feature를 업데이트하는 "refinement stage", 총 두 단계로 구성된다. TAP-Vid 벤치마크에서 기존 방법론들보다 월등하게 성능 향상을 이뤘고 재생시간이 길고 고해상도인 영상 데이터에 대해서도 빠른 추론시간을 확보했다고 주장한다.

➡️ Introduction

  TAP 모델은 영상데이터와 query point를 입력으로 받았을 때, 모든 frame에 대해서 해당 query point가 어디에 위치하는지 출력할 수 있어야 한다. 만약, query point가 다른 사물에 가려졌다가(occluded) 다시 나타나는 경우에 모델은 사라진 시점과 재등장한 시점을 인식할 수 있어야 한다. 게다가 잘 labeling된 현실 데이터의 양이 부족해서 대부분 임의로 생성한 데이터를 사용해 학습하는데, 이러한 방식은 overfitting의 위험이 있다.

  본 논문에서는 TAP을 잘 수행하기 위해 아래 3가지 주요 구조를 기반으로 설계한 TAPIR 모델을 제안한다.

1. Coarse-to-fine approach
   • 초반부에 등장하는 coarse tracking에서는 track은 저해상도에서 찾을 수 있다는 가정을 통해, 모든 frame에 대해서 occlusion에 강건한 매칭 방식을 사용
   • 이후 fine refinement 단계에서는 고해상도에서 국지(local)적인 시공간 정보를 반복적(iteratively)으로 사용
   • 위 두 방식을 통해 모델 네트워크는 smoothness of motion과 local apperance cue를 적당히 절충해서 학습
2. Fully-convolutional in time
   • 해당 네트워크 구조는 feature들을 비교하고, 시간적 convolution, 공간적 convolution을 수행
   • 현대의 GPU와 TPU에 효율적으로 mapping 되도록 구현  
3. Self-supervised estimation
   • 모델은 trajectory를 추정함에 있어, 자기 자신의 불확실성(uncerntainty)를 함께 추정할 수 있게 설계함
   • 즉, Self-supervised 방식의 도입을 통해 낮은 신뢰도를 갖는 예측 결과를 억제하는 효과

위의 설계 내용을 어느정도 만족하는 두 가지 모델이 이미 개발되어 있는데, 이는 TAP-Net과 Persistent Independent Particles(이하 PIPs)이다. 따라서 본 논문에서 제시한 구조는 이 두 모델의 장점을 효과적으로 결합하여 만들었다. 

• TAP-Net
  • 모든 frame에 대한 global search 수행
  • Occlusion에 강건한 coarse track을 예측
  • 영상데이터의 연속성을 올바로 활용하지 못해서 불안정하고 비현실적인 track을 예측
• PIPs
  • 주어진 Initialization에 따라, 주변 정보를 탐색해서 track을 부드럽게 예측
  • 영상데이터를 chunk 단위로 잘라서 진행되기 때문에, 각 chunk 예측을 위해 이전 chunk 계산 값이 필요
  • Occlusion을 잘 탐지하지 못하고, 병렬 계산을 하기 힘들어서 속도가 느림

➡️ Related Work

(중략)

➡️ TAPIR Model

TAPIR 모델의 입/출력과 개괄적인 Model Flow 및 특징은 아래와 같다.

• 입력
  • 영상(video)데이터
  • track 예측을 수행할 query point
• 출력 ( 모든 frame \({t}\)에 대한 )
  • 2D 위치 값 - query point에 대응하는 위치 \({p}_t\)
  • 1D 확률 값 - 위치 값의 가려진(occluded) 정도 \({o}_t\)
  • 1D 확률 값 - 위치 값의 불확실도(uncerntainty) \({u}_t\)
• Model Flow ( * 각 Stage에 대한 더 자세한 내용은 아래에서 설명 )
  • Stage 1. Track Initialization
    1. Occlusion에 강건하도록 각 frame의 후보 위치들을 모든 다른 frame의 query feature과의 similairty 비교를 통해 cost volume 계산 
       • query feature \({F}_q\)와 다른 모든 frame \({t}\)의 feature들을 각각 내적
       • 이때 모든 frame과의 내적을 수행하기 때문에, 시간적 연속성은 고려되지 못함
    2. 후처리를 통해 다음 Stage2.의 입력으로 필요한 형태로 변환
       • ConvNet을 통한 후처리로 cost volume을 spatial heatmap을 거쳐 point estimate로 변환함
       • TAP-Net의 방법론과 비슷하게 진행
  • Stage 2. Iterative Refinement
    1. query feature와 initial track의 주변 영역(small region)의 모든 feature 사이의 local similiarity를 계산
    2. query feature와 track을 업데이트
       • fully-convolutional pyramid구조를 통해 앞서 계산된 local similiarity를 전달해서 업데이트 수행
       • TAPIR의 최종 trajectory 예측 값을 출력하기 위해 이 과정을 수 차례 반복 수행
• 공통적인 특징 
  • 두 stage는 모두 query point feature와 다른 feature 사이의 내적(dot product)을 통한 similairty 계산을 사용하기 때문에, 해당 모델은 특정한 feature에 overfitting 되지 않음
  • track 예측 위치의 불확실도(uncerntainty)를 함께 추정하도록 설계함으로써 Self-supervised 하게 낮은 정확도를 갖는 예측을 억제

✔️ Track Initialization

 Initial cost volume은 TSM-ResNet backbone을 통해 계산된 coarse 한 feature map \({F} \in \mathbb{R}^{T \times \ H/8 \times W/8 \times C} \)를 사용해서 계산된다. 이때 \({T}\)는 총 frame 수, \({H}\)와 \({W}\)는 이미지의 높이와 너비, \({C}\)는 채널 수이다. 각 query point에 대한 query feature \({F}_q\)는 query location에서의 bilinear interpolation을 통해 구해지고, cost volume은 query feature와 다른 모든 feature 사이의 내적을 통해 계산된다. 

위치 \({p}^0_t=(x^0_t, y^0_t)\)에서의 initial estimate와 occlusion \({o}^0_t\)은 작은 ConvNet을 통해 계산된다. 이때의 입력은 frame \({t}\)에 대한 cost volume(query 당, \({H/8 \times W/8 \times1}\)) 이고 출력은 예측한 위치에 대한 heatmap( \({H/8 \times W/8 \times1}\))과 average pooling을 통해 얻어지는 occlusion을 추정하는 단일 scalar logit 값이다. Heatmap은 "spatial soft argmax"를 통해 position estimate로 변환된다. 즉, 이는 공간에 대해서 softmax를 하는 과정이며 heatmap의 값을 모두 합했을 때 1이 되도록 하는 양수 값들로 변환하는 효과를 갖는다. 그 이후 heatmap내의 값들 중 최고 값을 갖는 위치를 기준으로 멀리 떨어져 있는 값들은 모두 0으로 변경된다. heatmap은 thresholded heatmap magnitude에 의해 공간적 평균을 취하게 된다. 따라서 출력은 보통 heatpmap의 최대치에 가까운 값들이다. "soft argmax"는 미분가능하며 thresholding을 통해서 잘못된 matching을 억제한다.

Position Uncentainty Estimates

cost volume으로부터 position과 occlusion을 각각 독립적으로 예측하는 방식은 단점이 있다. 예를 들어 만약 point가 실제(ground truth)에서 잘 보이는 상태(visible)인데, 모델이 "완전히 잘못된 곳에 point가 있다고 예측하는 경우"가 단순히 "보이지 않는다고 판단하는 경우(invisible)" 보다 더 좋지 않을 수 있다. 

downstream application에서는 예측된 track을 통해 object motion을 이해하고 싶을 것이다. 이러한 downstream pipeline은 occlusion에 강건해야 하지만,  occlusion을 잘 고려하지 못한 경우에도 잘 예측한 결과라고 착각할 수 있다. Average-Jaccard 평가지표는 이러한 맹점을 해결할 수 있는데, 잘못된 예측을 한 경우에 "false positive"와 "false negative"로 둘 다 카운트하는 방식이다.

위와 같은 단점은 알고리즘의 위치 추정에 대한 불확실성이 클 때 주로 발생한다. 그러므로 저자는 position 예측과 함께 예측 자체에 대한 불확실도를 함께 산출되도록 설계했다. 모델이 예측하는 position이 ground truth에서 threshold \({\delta}\) 보다 더 멀리 떨어져 있다면  불확실도 \({u}^0_t\)를 1로 산출하는 방식이다. 

결과적으로 frame \({t}\)에 대한 최종 loss \( \mathcal{L}(p_t^0, o_t^0, u_t^0) \)는 아래와 같이 정의된다.

$\begin{array}{rl}{{\mathcal{L}}(p_{t},o_{t},u_{t})} & {=\operatorname{Huber}({\hat{p}}_{t},p_{t})*(1-\hat{o}_{t})}\\ {} & {\quad\operatorname{+BCE}({\hat{o}_t, o_t})}\\ {} & {{\quad\operatorname{+BCE}({\hat{u}}_{t},u_{t})*(1-{\hat{o}}_{t})}}\\ {\operatorname{where},\quad{\hat{u}}_{t}} & {{=\begin{cases}{\begin{array}{lc} {1}&\text{if} \;\; d(\hat{p}_t), p_t) > \delta \\ {0}&\text{otherwise} \end{array}}\end{cases}}}\end{array}  \tag{1}$

\(\hat{o}_t \in \{0, 1\} \)과 \(\hat{p} \in \mathbb {R}^2\) 은 각각 occlusion정도와 point의 위치에 대한 ground truth이다. \({d}\)는 Euclidean 거리이며 \({\theta}\)는 불확실성 구분을 위한 threshold이다. \(\operatorname {Huber}\)는 Huber loss이고 \(\operatorname{BCE}\)는 binary cross entropy이다 (\({o}_t\)와 \({u}_t\)를 확률값으로 해석하기 위해서 sigmoid를 적용). \(\hat{u}_t\)는 예측된 불확실도 \({u}_t\)의 target이 되는데, 이는 ground truth 위치와 예측된 위치 사이의 거리에 따라 결정된다 (예측 위치가 ground truth를 기준으로 \({\delta}\)보다 적은 거리 내에 있는 경우에 0이 됨).

테스트를 진행할 때, 모델은 point가 보이는지 아닌지 여부를 함께 출력하는데, \({(1-u_t) \ast (1-o_t)} > 0.5\)를 만족할 경우 보이는 것으로 간주한다.

✔️ Iterative Refinement

모든 frame에 대해서 position, occlusion, uncentainty 값이 예측된 이후, refinement를 위한 각 iteration \({i}\)의 목표는 estimation을 좀 더 ground truth에 근접하도록 모든 frame의 정보들을 이용해 \((\Delta{p_t^i}, \Delta{o_t^i}, \Delta{u_t^i} )\)를 계산함으로써 업데이트하는 것이다. 이 업데이트는 query point feature와 그 주변부의 feature들 사이의 유사도(내적과 같은) 계산을 통해 만든 local score maps를 바탕으로 진행된다. local score maps는 해상도(resolution) 별로 pyramid 구조를 통해 계산되는데, 주어진 trajectory에 대해서 \(({H^\prime} \times {W^\prime} \times {L})\) ( \({H}^{\prime} = {W}^{\prime} = 7 \) ), local neighbor의 크기)의 shape을 가지고 \({L}\)은 spatial pyramid의 층 수이다. 이때 다른 층의 값은 feature를 pooling으로 층에 맞게 사이즈 조절을 하고 나서 계산된다.

Track initialization과 마찬가지로 local score maps도 후처리 layer를 통해서 refine 된 position, occlusion, uncentainty를 예측하게 되는데, 이때의 차이점은 local score maps를 사용할 때 모든 frame의 정보를 동시에 후처리 layer의 입력값으로 사용한다는 점이다. 즉 이 후처리 layer의 입력은 현재 iteration에서의 position estimate, 원본 query feature, flatten 된 local score maps이고 shape은 \({T} \times (C+K+4)\)이다 (\({C}\)는 query feature의 채널 수, \({K = {H}^{\prime} \cdot {W}^{\prime} \cdot {L}}\))는 local score map의 flatten된 값 개수, 4는 position, occlusion, uncerntainty를 위해 추가된 차원 수). 또한 \({i}\) 번째 iteration에서 후처리 layer의 출력은 \( ( \Delta{p}_t^i, \Delta{o}_t^i, \Delta{u}_t^i, \Delta{F}_{q,t,i}) \) 이고 각각 position, occlusion, uncentainty, query feature에 대헤 업데이트하기 위한 값이다. \( \Delta{F}_{q,t,i} \)는 \({T} \times {C}\)의 shape을 갖는데, 첫 번째 iteration 이후에는 이 업데이트 값이 반영된 query feature를 입력에 다시 사용하게 된다.

위에 설명한 일련의 과정과 같이 position과 score maps는 총 12 블록의 ConvNet에 입력되어 \( ( \Delta{p}_t^i, \Delta{o}_t^i, \Delta{u}_t^i, \Delta{F}_{q,t,i}) \) 가 계산되고, 각 블록은 \(\text{1} \times \text{1}\) convolution 블록과 depthwise convolution 블록으로 구성된다. 이러한 구조는 PIPs의 refinement 과정에서 사용된 MLP-Mixer를 통해 영감을 얻었는데, 본 논문에서는 Mixer의 cross channel layer를 같은 채널 수를 사용하는 \(\text{1} \times \text{1}\) convolution 블록으로 대체했고 채널 내의 연산을 depth wise convolution으로 변경했다. 또한 MLP-Mixer의 입력으로 영상데이터를 8-frame 별 chunk로 잘라서 사용하는 PIPs와는 다르게, 본 논문에서 변경한 convolutional 구조는 어떠한 길이의 영상데이터를 가지고도 입력으로 사용할 수 있다.  

Score maps을 계산하기 위해 사용되는 feature maps는 높은 성능 확보를 위해 중요하다는 사실을 발견했다. Pyramid 구조의 \({l} = 1\) 층부터 \({L} - 1\) 층까지의 score maps는 1) TSM-ResNet을 통해 계산된 raw feature \({F}\)에 \({8} \cdot {2}^{l-1}\) 크기의 stride를 사용한 average pooling을 적용한 feature와 2) query feature \({F}_q\) 사이의 내적을 통해 계산된다. 결과적으로 각 \({t}\) 번째 frame에 대해서, \({p_t}\)를 중심으로 \({7}\times{7}\) 크기를 갖는 내적 patch를 뽑게 된다.

모델의 학습시간에 PIPs는 위와 같이 진행하지만, 테스트를 할 때는 backbone의 stride를 4로 변경하는데, 이는 train/test domain gap을 보여주기 위한 방법이다. 본 논문의 저자는 학습 시에도 stride 4를 사용하는 것이 효과적인 것을 발견했는데 이 방식은 system의 메모리를 많이 사용한다는 단점이 있다. 따라서 이 점을 개선하기 위해 초기의 score map를 64 채널 stide 4를 사용하는 TSM-ResNet을 통해 계산한 뒤 bilinear interpolation을 통해 상응하는 feature를 뽑는 방식을 사용했다. 따라서 최종 local score maps는 \( ( {7}\cdot{7}\cdot{L} ) \)의 shape을 갖게 된다.

위에서 설명한 구조를 통해 \( ( \Delta{p}_t^i, \Delta{o}_t^i, \Delta{u}_t^i, \Delta{F}_{q,t,i}) \) 를 얻게되어 반복적으로 refinement를 수행할 수 있다.

⚠️ 온전한 이해를 위해서 TAPIR 논문 리뷰 선행 권장

Paper link : https://arxiv.org/abs/2402.00847

➡️ Abstract

• Tracking-Any-Point(이하 TAP) : 비디오 데이터에서 조밀한 시공간 내의 특정 지점을 추적하는 알고리즘
• 해당 논문에서는 실제 large-scale, unlabeled, uncurated 데이터를 사용한 self-supervised learning을 통해서, 약간의 모델 구조 변화로도 TAP 모델의 성능 향상이 가능하다는 점을 시사함
• TAP-Vid benchmark의 기존 SOTA 모델 성능을 크게 뛰어넘었음
  • TAP-Vid-DAVIS : 61.3% → 66.4%
  • TAP-Vid-Kinetics : 57.2% → 61.5%

➡️ Introduction

• 최근 vision 모델의 발전이 지속되고 있으나, 여전히 물리 공간적인 추론 능력 부족이 SOTA 모델들의 약점
• 복잡한 움직임과 물리적인 상호작용을 이해해야 하는 robotics, video generation/editing, 3D asset creation와 같은 작업에서 TAP은 정확한 움직임을 표현하기 위한 유망한 알고리즘
  • 고체 표면에 대해서 일치하는 점을 추적하는 방식을 통해, 물체의 deformation과 motion에 대한 가치 있는 정보를 얻을 수 있음
• TAP은 비디오 데이터와 움직임 추적을 위한 query point 집합을 입력으로 받고, 비디오의 매 frame 마다 해당 query point들의 추적된 위치를 출력해야 함
  • 만약 중간에 query point가 사라지는 경우, 해당 frame에서 point가 투명해진(occluded) 정도도 함께 모델링함
• TAP 모델을 만들기 어려운 이유는 현실적인 training data의 부족
  • 이유 1: 부정확하고 균일하지 못한 수동 labeling 방식
  • 이유 2: 특수한 상황에서만 사용할 수 있는 3D sensing 방식
  • 따라서, 현재 SOTA 모델은 임의 생성(synthetic) 데이터에 의존
• 해당 논문은 unlabeled 데이터를 사용해서 TAP 성능을 향상하는 방식을 제안
  • 만약 주어진 video에 대한 추적이 잘 이루어졌다면 아래 3가지 항목들이 지켜져야 함 (지켜지지 않아서 생기는 error를 학습을 위해 사용)
    1. video와 trajectory에 대한 spatial transformation이 동일
    2. 동일한 trajectory 위에 존재하는 query point들은 동일한 추적값 산출
    3. 이미지 압축과 같이 비공간적인 데이터 augmentation을 한 경우, 동일한 결과 산출

➡️ Method

self-training TAP을 개발함에 있어서 저자는 optical flow와 비슷하게 TAP도 query point들에 대한 정확한 정답이 존재한다는 점에 주목했다. 이는 의미적으로 비슷한 이미지가 비슷한 표현을 갖는 한, 다른 self-supervised 방법론과는 구분되는 특징이다. 

제시한 방법론은 단단하고 불투명한 표면 위의 point 추적에 대해서 아래 두 가지 조건에 기반한다.

1. affine tranformation과 같은 spatial transformation를 video에 적용한 결과와 point tracks(trajectory)에 적용한 결과는 동일
2. track 위의 어떤 point를 query로 사용하더라도 산출되는 결과는 동일

저자는 위의 두 조건을 만족시키기 위해 Siamess 구조를 사용할 수 도 있지만, 이러한 방법은 예측 결과 성능이 좋지 않았다고 한다. 대신 Student-Teacher 구조를 사용했는데, student는 augmentation을 통해 더 어려운 데이터를 입력으로 받고 teacher은 gradient를 전달받지 않는 것이 특징이다.

모델은 Kubric 데이터 셋으로 pre-trained된 TAPIR network로 시작된다. 모델의 예측값을 \(\hat{y}=\{\hat{p}[t], \hat{o}[t] , \hat{u}[t]\}\)라 하자. 이때 \(\hat{p}\in\mathbb{R}^{T\times2}\)는 위치값(position), \(\hat{o}\in\mathbb{R}^{T}\)는 투명도(occlusion logit), \(\hat{u}\in\mathbb{R}^{T}\)는 불확실도(uncentainty logit)이고 \({T}\)는 frame수 이다. \({p[t]}\)와 \({o[t]}\)는 frame \({t}\)에서의 ground truth이고, 하나의 trajectory에 대한 TAPIR loss는 아래와 같이 정의된다.

$ \begin{array}{rlr}{{\mathcal{L}_{tapir}}(\hat{p}[t],\hat{o}[t],\hat{u}[t])} & {=\operatorname{Huber}({\hat{p}}[t],p[t])(1-\hat{o}[t])} & \text{Position loss}\\ {} & {\quad\operatorname{+BCE}({\hat{o}[t], o[t]})} & \text{Occlusion loss}\\ {} & {{\quad\operatorname{+BCE}({\hat{u}}[t],u[t])(1-{\hat{o}}[t])}} & \text{Uncertainty loss}\end{array}  \tag{1}$

불확실도(uncerntainty logit)는 \({u[t]}= \unicode{x1D7D9} (d(p[t],\hat{p}[t] > \delta))\)으로, \({d}\)는 \({L}_2\) 거리이며 \({\delta}\)는 6 pixel로 설정된 거리의 threshold 값이고 \({ \unicode{x1D7D9} }\)는 특성 함수(indicator function)이다. 즉, 불확실도는 모델의 예측값이 ground truth의 근처(threshold 만큼)에 위치하게끔 학습하게 하는 효과를 준다. 

pre-training 이후에는 추가 convolutional residual layer를 추가해서 추가 학습 데이터를 입력받을 수 있게 한다. \(\hat{y}_\mathcal{S}=\{\hat{p}_ \mathcal{S} , \hat{o}_ \mathcal{S} , \hat{u}_ \mathcal{S} \}\)를 student의 예측값이라고 하고, teacher의 예측 \(\hat{y}_\mathcal{T}=\{\hat{p}_ \mathcal{T} , \hat{o}_ \mathcal{T} , \hat{u}_ \mathcal{T} \}\)으로 부터 pseudo-labels \({y}_\mathcal{T}=\{{p}_ \mathcal{T} , {o}_ \mathcal{T} , {u}_ \mathcal{T} \}\)를 뽑는다. ( \({t}\)는 시간 index )

$ p_\mathcal{T}[t]=\hat{p}_\mathcal{T}[t]\quad;\quad o_\mathcal{T}[t]=\unicode{x1D7D9}(\hat{o}_\mathcal{T}[t]>0);\quad u_\mathcal{T}[t]= \unicode{x1D7D9}(d(p_\mathcal{T}[t],\hat{p}_\mathcal{S}[t])>\delta) \tag{2} $

video frame \({t}\)에서의 loss값 \({\ell_{s s l}(\hat{p}_\mathcal{S}[t], \hat{o}_\mathcal{S}[t], \hat{u}_\mathcal{S}[t])}\) 는 TAPIR loss로부터 구할 수 있고, 이는 pseudo-label로써 ground truth로 사용하며 다음과 같이 정의된다.

$  \begin{array}{rl}{{\ell_{tapir}}(\hat{p}_\mathcal{S}[t],\hat{o}_\mathcal{S}[t],\hat{u}_\mathcal{S}[t])} & {=\operatorname{Huber}({\hat{p}}_\mathcal{S}[t],p_\mathcal{T}[t])(1-{o}_\mathcal{T}[t])} \\ {} & {\quad\operatorname{+BCE}({\hat{o}_\mathcal{S}[t], o_\mathcal{T}[t]})} \\ {} & {{\quad\operatorname{+BCE}({\hat{u}}_\mathcal{S}[t],u_\mathcal{T}[t])(1-{{o}}_\mathcal{T}[t])}} \end{array}  \tag{3} $

TAPIR의 loss는 여러 번 refinement iteration을 거치게 되고, teacher의 마지막 단계의 refine 된 예측값을 ground  truth로 사용하기 때문에 refine 되지 않은 데이터가 더 빠르게 수렴할 수 있게 돕는 역할을 할 수 있다.

만약 위의 식이 잘 정의되었다면 student와 teacher가 동일한 video query point를 입력받았을 때, loss 값은 아주 작아야 한다. 이러한 특성을 학습하게 하기 위해서 input video query에 대해서 affine tranformation과 같은 \({\Phi}\)를 pixel에 적용시켜서 낮은 resolution을 갖도록 사이즈를 줄이고, 예측을 더욱 어렵게 하기 위해 JPEG degradation을 적용한 이미지를 student에 전달하여 track을 연산하게 한다. 출력 값에 \({\Phi}^{-1}\)를 적용시켜 입력 좌표공간으로 되돌린 다음 teacher의 track과의 비교를 통해 loss를 계산한다.

또한 저자는 동일한 같은 track 위의 query points 짝에 대해서 teacher의 두 예측값이 같은 값을 출력하도록 하도록 frame별 loss 함수를 수정하는 두 가지의 계수를 추가했다. 첫 번째로, 먼저 \(Q_1 = (q_1, t_1)\)을 뽑았는데 \(q_{1}\)은 \({(x, y)}\)형식의 좌표이고 \({t_1}\)은 frame index이며 두 값은 랜덤하게 sampling한다. 그 후에 student의 query는 teacher의 trajectory 위에서 랜덤하게 뽑는다. (\({i.e.}\quad Q_2=(q_2,t_2)\in\{(p_\mathcal{T}[t],t);t \quad s.t. \quad o_\mathcal{T}[t]=0\}\))

하지만 teacher가 query point를 잘 추적(track) 하지 못하는 경우가 있을 수 있는데, 그럴 경우 student는 더더욱 추적을 잘하지 못할 것이다. 이러한 경우를 막기 위해서 저자는 cycle-consistency를 도입했다. valid 한 trajectory를 구분하는 mask를 계산해서 valid 하지 않은 경우는 loss 계산을 하지 않고 무시하는 방법인데, 이때 사용되는 mask는 다음과 같이 정의된다. ( \(\delta{cycle}\)은 거리 threshold이며, 저자는 4 pixel을 사용했다, 위 Fig. 2의 주황 원형 영역 참고 )

$ m_{c y c l e}= \unicode{x1D7D9} \left(d({\hat{p}}s[t_{1}],q_{1}\right)<\delta_{c y c l e})\quad*\quad \unicode{x1D7D9} \left(\delta s[t_{1}]\leq0\right) \tag{4} $

두 번째로, frame index \({t}\)의 위치에 따른 정확도 차이를 고려하는 proximity를 도입했다. 저자는 student의 query frame에 가까운 포인트들에 대해서는 teacher의 예측값보다 student의 예측값이 더 정확할 것이라고 생각했다. 이를 반영해서 정의한 mask는 다음과 같다. ( Fig. 2의 회색 사각 영역 참고 ) 

$ m^t_{proximity}= \unicode{x1D7D9}(|t-t_1| \leq |t-t_2|) \tag{5} $

위 \({(4)}\)와 \({(5)}\)를 통해 계산한 최종 loss는 아래와 같다.

$ \mathcal{L}_{S S L} = \sum\limits_{t}{m}_{\scriptscriptstyle{c y c l e}}^{t} \ast m_{p r o x i m i t y}^{t}\ast\ell_{\scriptscriptstyle{S S l}}^{t} \tag{6} $

Paper link : https://proceedings.neurips.cc/paper_files/paper/2015/hash/33ceb07bf4eeb3da587e268d663aba1a-Abstract.html

➡️ Abstract

  CNN은 강력한 모델로 떠올랐지만, 여전히 입력 데이터에 대해 Spatial Invariance에 대한 계산 능력과 효율적인 파라미터 유지 능력이 부족하다는 한계가 있다. 본 논문에서는 추가적인 지도 학습이나 최적화 과정 없이도 feature map을 변환할 수 있는 학습가능한 모듈 Spatial Transformer를 연구했다. 이미지의 변환, 크기 조정, warping 등에 대한 Spatial Invariance를 효과적으로 학습할 수 있는 효과적인 모듈을 제안한다.

( * Spatial Invariance : 임의 변환된 입력 이미지에 대해서, 동일한 원본 이미지로 인식할 수 있는 성질 )

➡️ Introduction

  CNN의 발전으로 Computer vision 분야는 큰 발전을 이룩했다. 비록 새로 개발된 모델 구조는 아니었지만, 이를 구조를 응용해서 Classfication, Localisation, Sematic Segmentation, Action Recogition 등 다양한 분야에서 최고의 성능을 확보할 수 있었다. 

  이미지 데이터를 추론하는 모델에게 기대하는 속성 중 하나는, Object의 질감과 모양으로부터 자세나 부분의 변화를 분리하는 것이다. CNN은 Max-pooling layer를 사용함으로써 위와 같은 속성인 Spatial invariance를 확보할 수 있었는데, 만약 입력 이미지 데이터에서 변화하는 부분이 너무 작거나 큰 경우에는 잘 인식하지 못하는 한계가 있었다.

  본 논문에서 소개하는 Spatial Transformer 는 모델이 공간적인 변화를 잘 인지할 수 있게 만들어주는 모듈인데, 일반적인 neural network 구조에 쉽게 추가해서 사용할 수 있다. 또한 고정된 receptive field를 갖는 pooling layer와는 달리, Spatial Tranformer는 동적으로 적절한 변화점을 인식할 수 있게 해준다. 이러한 특성으로 인해서 단순히 변화가 일어나는 지점을 찾는 것 뿐만 아니라, 다음 layer의 연산을 돕기 위해 feature를 일반적으로(canonical) 변환하는 기능도 수행할 수 있다.

Spatial Transformer는 CNN 구조에 결합되어 다음과 같은 다양한 작업에 활용될 수 있다.

• Image Classifcation
  • Figure1과 같이 숫자의 위치나 크기가 모두 다른 sample들에 대해서 Classifcation 과정이 원활하게 진행될 수 있도록 해당 모듈을 사용할 수 있다.
• Co-localisation
  • 동일한(단, 알 수 없는) 클래스의 다른 인스턴스를 포함하는 이미지 집합이 주어지면, 해당 모듈을 통해 각 이미지에서 인스턴스를 위치 지정하는데 활용될 수 있다.
• Spatial Attention
  • Attention 메커니즘을 필요로 하는 작업에 사용될 수 있는데, 이로 인해 낮은 해상도의 이미지를 고해상도의 이미지 처럼 사용할 수 있게 되어 계산 속도에서 이점을 가질 수 있다.

➡️ Related Work

( 중략 )

➡️ Spatial Tranformers

  Spatial Transformer는 feed-forward 단계에서 하나의 feature map을 입력으로 받고 내부적으로 공간 변화 연산을 수행하며 하나의 feature map을 출력하는 미분가능한 모듈이다. 여러 channel을 갖는 입력의 경우에는, 각 channel에 대해 동일한 기능을 각각 수행한다. 단, 이 섹션에서는 설명의 편의를 위해서 입력 데이터는 하나의 channel을 갖는다고 가정한다. 

✔️ Localisation Network

  Localisation network은 입력으로 feature map \({U \in \mathbb{R}^{H \times W \times C}}\)을 받고 (\({W}\)는 너비, \({H}\)는 높이, \({C}\)는 channel 수), 출력으로는 \({\theta}\)를 반환한다. 출력 \({\theta}\)는 이후에 있을 변환 \({\mathcal{T}}_\theta\) 의 파라미터로, \({\theta} = f_{loc}(U)\)로 표현된다. \({\theta}\)의 크기는 변환의 종류에 따라서 달라질 수 있다. 예를 들어 Affine 변환의 경우 \({\theta}\)는 6차원을 갖는다.

✔️ Parameterised Sampling Grid

  입력 feature map에 대한 warping 연산은 각 출력 "pixel"은 feature map의 특정 위치를 중심으로 하는 sampling kernel을 통과함으로써 계산된다. 여기서 "pixel"이라는 표현은 꼭 원본 이미지에서의 픽셀을 뜻하는것에 국한되지 않고, feature map에서의 픽셀도 아우른다. 일반적으로 출력 pixel들은 regular grid \(G = \{ G_i \} \) 위에 있는 것으로 정의되는데 ( \({G_i = ({x}^t_i, {y}^t_i))}\) ), 이때 출력 pixel들이 모여서 출력 feature map \({U \in \mathbb{R}^{H^{\prime} \times W^{\prime} \times C}}\) 를 구성한다. (\({W}^ {\prime} \)는 grid의 너비, \({H}^ {\prime} \)는 grid의 높이, \({C}\)는 입력 feature map에서와 동일한 channel수)

  설명의 편의를 위해서 \({\mathcal{T}}_\theta\)는 2차원 Affine 변환 \({\mathbf{A}_\theta}\)라고 가정한다. (다른 변환들은 아래에서 재차 다룰 예정)  

$ \left(\begin{array}{c}x_i^s \\ y_i^s\end{array}\right)=\mathcal{T}_\theta\left(G_i\right)=\mathrm{A}_\theta\left(\begin{array}{c}x_i^t \\ y_i^t \\ 1\end{array}\right)=\left[\begin{array}{lll}\theta_{11} & \theta_{12} & \theta_{13} \\ \theta_{21} & \theta_{22} & \theta_{23}\end{array}\right]\left(\begin{array}{c}x_i^t \\ y_i^t \\ 1\end{array}\right) \tag{1} $

\({(1)}\)번 식은 Affine 변환으로, pointwise transformation의 예시이다. \({ ({x}^t_i, {y}^t_i) }\)는 출력 feature map에서 grid의 target 좌표이고,  \({ ({x}^{s}_i, {y}^{s}_i) }\)는 입력 feature map에서 정의된 source 좌표이다. 이때 각 입출력 공간에서의 높이와 너비는 정규화된 값을 사용한다 \(( -1 \leq {x}_i^s, {y}_i^s \leq 1, \;\; -1 \leq {x}_i^t, {y}_s^t \leq 1 )\) 

$ \mathrm{A}_\theta=\left[\begin{array}{ccc}
s & 0 & t_x \\
0 & s & t_y
\end{array}\right] \tag{2} $

위와 같이 변환 \({\mathcal{T}}_\theta\)는 더 제한적(constrained)일 수 있는데, 다양한 \({s}, {t}_x, {t}_y\)의 값 변화에 따라  cropping, translation, isotropic scaling과 같은 변환 효과를 얻을 수 있다. 이 parameter가 8개가 되면 평면에 projection시키거나 piece-wise 아핀 변환, thin plate spline과 같이 조금 더 일반적인 변환도 할 수 있다. 앞선 내용들을 정리하면, 변환에 사용되는 parameter들이 어떻게 설정되냐에 따라 다양한 변환을 표현할 수 있고 이 parameter들이 미분가능하도록 구현하면 backpropagation을 통해 localisation network 출력 \({\theta}\)를 학습을 할 수 있다는 것이다. 예를들어 attention, affine, projection, thin plate spline 변환들이 표현 가능한 일반적이면서도 미분가능한 변환 \({\mathcal{T}}_\theta = M_{\theta}B\)가 있을 때, \({B}\)는 \({(1)}\)번 식에서 G와 동치로 target grid를 의미하며 \({M_\theta}\)는 \({\theta}\)로 parametrized 된 행렬이다. 이 경우에 입력 데이터에 대해서 \({\theta}\)를 학습을 할 수 있고, 작업의 종류에 따른 \({B}\) 행렬도 학습할 수 있다.

✔️ Differentiable Image Sampling

입력 feature map에 대해서 공간 변환을 수행하기 위해, sampler는 입력 feature map \({U}\)를 따라 샘플링된 점들의 집합인 \({\mathcal{T}}_{\theta}(G)\)를 입력받고 샘플링된 출력 feature map \({V}\)를 반환해야 한다. 모든 \({i}\)에 대해서 \(\mathcal {T}_\theta(G)\) 위의 \(({x}_i^s , {y}_i^s)\) 좌표들은 sampling kernel을 통과하여 output feature \({V}\) 위의 특정한 pixel로 변환된다. 이는 아래와 같은 식으로 표현할 수 있다.

$  V_i^c=\sum_n^H \sum_m^W U_{n m}^c k\left(x_i^s-m ; \Phi_x\right) k\left(y_i^s-n ; \Phi_y\right) \forall i \in\left[1 \ldots H^{\prime} W^{\prime}\right] \forall c \in[1 \ldots C] \tag{3} $

\({\Phi}_x\)와 \({\Phi}_y\)는 bilinear interpolation과 같이 일반화된 sampling kernel \(k\left(\right)\)의 parameter이다. \({U}_{nm}^c\)는 입력 데이터의 \({c}\)번 째 channel에서 \((n, m)\) 위치 값이고, \({V}_i^c\)는 \({c}\)번 째 channel의 \(({x}_i^t, {y}_i^t)\) 위치의 \({i}\) 번 째 pixel 출력 값이다. sampling 연산은 모든 channel에 대해서 독립적으로 수행됨으로써, channel 사이의 spatial consistency가 유지된다.

이론적으로 \({x}_i^s\) 와 \({y}_i^s\)에 대해서 미분이 가능하다면 다른 어떠한 sampling kernel을 사용해도 무방하다. 아래는 \({(3)}\) 번 식에 integer sampling kernel을 적용한 예시이다.

$ V_{i}^{c}=\sum_{n}^{I I}\sum_{m}^{W}U_{n m}^{c}\delta(\lfloor x_{i}^{s}+0.5\rfloor-m)\delta(\lfloor y_{i}^{s}+0.5\rfloor-n) \tag{4} $

\(\lfloor x+0.5\rfloor\) 는 \({x}\)를 가장 가까운 정수로 반올림(0.5를 더해준 다음 내림하게 되면 반올림을 하는 것과 같음)해주고 \({\delta}\) 는 Kronecker delta function이다. 이 kernel은 단순히 \(({x}_i^s, {y}_i^s)\) 에서 가장 가까운 pixel을 \(({x}_i^t, {y}_i^t\)로 복사하는 역할을 한다. 또 다른 예로는 bilinear sampling kernel을 사용하는 것이고, 그 식은 아래와 같다.

$  V_{i}^{c}=\sum_{n}^{I}\sum_{m}^{W}U_{n m}^{c}\,\mathrm{^{max}}^{}(0,1-\left|x_{i}^{s}-m\right|)\,\mathrm{max}(0,1-\left|y_{i}^{s}-n\right|) \tag{5} $

앞서 언급한 것 처럼 결국 sampling을 수행하면서 backpropagation을 가능하게 하려면, \({U}\) 과 \({G}\)에 대해서 미분가능해야한다. \({(5)}\) 번 식을 편미분하게 되면 아래와 같은 식을 얻을 수 있다.

$ \frac{\partial V_{i}^{c}}{\partial U_{n m}^{c}}=\sum_{n}^{H}\sum_{m}^{W}\mathrm{max}(0,1-|x_{i}^{s}-m|)\operatorname*{max}(0,1-|y_{i}^{s}-n|) \tag{6} $

$ \frac{\partial V_{i}^{c}}{\partial x_{i}^{s}}=\sum_{n}^{H}\sum_{m}^{W}U_{n m}^{c}\operatorname*{max}(0,1-|y_{i}^{s}-n|)\left\{\begin{array}{l l}{{0}}&{{\mathrm{if~}|m-x_{i}^{s}|\geq1}}\\ {{1}}&{{\mathrm{if~}m\geq x_{i}^{s}}}\\ {{-1}}&{{\mathrm{if~}m<x_{i}^{s}}}\end{array}\right. \tag{7} $

( \({(7)}\)번 식과 동일한 방식으로 \( \frac{\partial V_{i}^{c}}{\partial y_{i}^{s}} \)도 계산 가능하다. )

위 편미분 식을 통해 해당 sampling이 미분 가능하며 loss gradient를 입력 feature map과 sampling grid의 좌표로 backpropagate 할 수 있음을 보여준다. 따라서 더 이전의 localisation network의 parameter \({\theta}\)까지의 backpropagation도 가능하다 (식 \({(1)}\) 참고 ).  

✔️ Spatial Transformer Networks

앞서 설명한 세 모듈 localisation network, grid generator, sampler를 합쳐서 Spatial Transformer Network를 구성하게 된다. 이 네트워크 구조는 어떠한 CNN 아키텍쳐에도 적용될 수 있으며 사용되는 개수에도 제한이 없다. 해당 구조를 추가함으로 써, 모델은 기존 학습 과정 중간에 동적으로 전체 cost를 최소화하는 feature map을 변환 방식을 함께 학습한다. 또한 기존의 모델 속도에는 크게 영향을 미치지 않는다. 마지막으로 여러 개의 Spatial Transformer 구조를 CNN 구조가 깊어지는 중간에 사용하게 되면 모델이 더 추상적인 representation을 다루게하는 효과가 있다.  

Paper link : Link (본 포스트에 사용된 모든 이미지는 해당 논문에서 발췌하였습니다)

➡️ Abstract

• 본 논문은 Optical flow를 위한 가볍고 효과적인 CNN 기반의 PWC-Net 모델을 제안함
• 모델을 구성하는 모듈 (각 모듈에 대한 description은 아래 Approach에서 함)
  
  • Pyramidal processing
  • Warping
  • Cost volume
• 모델의 전체적인 흐름
  1. 학습 가능한 pyramid 모듈을 사용해서 두 번째 입력 이미지의 CNN feature를 현재 optical flow를 고려하여 warping한다
  2. warping된 feature와 첫 번째 입력 이미지의 feature을 사용한 cost volume을 통해 Optical flow를 추정한다
• 이전에 뛰어난 성능을 보였던 FlowNet2 모델 보다 약 17배 적은 사이즈를 가짐
• MPI Sintel final pass와 KITTI 2015 benchmarks 데이터에서 기존에 제안된 모든 방법론들 보다 뛰어난 성능 확보
• 코드 경로 : https://github.com/NVlabs/PWC-Net

➡️ Introduction

  Optical flow estimation은 computer vision 분야의 핵심 문제로 자리잡았고, 많은 연구와 응용 사례가 생기고 있지만, 많은 계산양으로 인해 실시간성의 한계를 갖고 있다. 비록 성능적으로 SOTA는 아니지만, U-Net 구조를 사용한 FlowNetC와 FlowNetS라는 실시간성을 확보한 모델이 등장하기도 했다. 이후에는 FlowNetC와 FlowNetS를 쌓아서 만든 FlowNet2가 성능적으로 SOTA를 달성했으나, 과도하게 큰 모델 사이즈(640MB)와 Overfitting이라는 한계점이 여전히 남아있었다. FlowNet2와는 반대로, 새롭게 등장한 SpyNet은 고전적 optimal flow estimation 방식인 pyramid와 warping을 deep learning에 접목시킴으로써 모델 사이즈는 작게 줄일 수 있었지만 좋은 성능은 확보하지 못했다(Trade-off between model size and accuracy).

  본 논문의 저자는 SpyNet을 통해 고전적인 방법론과 CNN 구조의 결합에 대한 가능성을 확인했고, SpyNet의 낮은 성능의 문제를 해결해서 모델의 사이즈도 작고 성능도 좋은 모델 개발을 위한 연구를 진행했다. 저자는 다음과 같은 두 가지 관점을 제시했다. 첫 번째는 전통적인 Optical flow 방식 자체의 한계를 지적했는데, raw image를 전처리하는 과정에서 변하는 조명이나 그림자에 영향을 받지 않는 feature만을 추출한다고 주장한다. 또한 두 번째로는 cost volume을 통해 raw image나 feature보다 더 descrimiative 한 정보를 뽑을 수 있다고 주장한다. 다만, 과도한 계산량이 요구되는 전체 cost volume 계산 대신 pyramid level과 warping을 통한 partial cost volume 방식을 제안한다. 

  논문에서 제시하는 PWC-Net은 위와 같은 단순하지만 잘 짜인 원리들을 고수하여 모델의 사이즈를 줄이면서도 좋은 성능을 확보할 수 있었다고 한다. 논문을 작성하던 시기에 MPI Sintel final pass와 KITTI 2015 benchmarks 데이터셋에 대해 제시된 다른 방법론들 중에 가장 좋은 성능을 확보했다고 하고, 모델의 사이즈는 FlowNet2 보다 17배가 작았다고 한다. 또한 SpyNet과 FlowNet2보다 학습시키기가 편하고, (1024 x 436) 크기의 이미지를 35 fps의 실시간 데이터를 처리할 수 있다고 한다.

➡️ Previous Work

✔️ Variational approach

Optical flow 분석을 위한 과거의 접근법의 변화 과정을 설명한다.

• Horn & Schunk : Energy function을 통해 밝기 불변성과 공간적 평활도를 결합하여 Optical flow 분야를 개척함
• Black & Anandan : 밝기의 불일치성과 공간적 비연속성과 같은 outlier를 고려하는 강건한 방법론 제시
• Brox & Sun : 기 제시된 방법론들의 과도한 계산량의 문제를 해결하기 위해서 warping 기반의 coarse-to-fine 방법론 제시 및 고도화
  • 다만, 여전히 실시간으로 작동하기에는 계산량이 많았음
• Brox & Malik : coarse-to-fine 방법론은 coarse 단계에서 아주 작거나 빠른 물체를 탐지하지 못한다는 단점이 존재했는데, 이를 해결하기 위해서 feature matching 방법론 제시
  • 이후 후처리 방식인 EpicFlow와 CNN 기반의 두 interpolation 방법론으로 고도화 
• 이후 DCFlow, FlowField-sCNN, MRFlow와 같은 다양한 CNN 기반의 고도화된 방법론이 등장했으나, 그 어떠한 모델도 실시간성을 확보하지 못했음

✔️ Recent work on learning optical flow

  CNN 기반의 모델들을 vision 과제에서 성공적으로 적용시킨 사례들에 영감을 받아서, 저자 Dosovitskiy는 U-Net denoising autoencoder를 기반으로 optical flow를 추정하는 두 CNN 모델 FlowNetsS와 FlowNetC를 개발한다. 두 모델은 FlyingChairs 데이터로 사전학습되었고 Sintel 데이터의 빠른 움직임을 갖는 물체들에 대해서 성공적으로 작동했다. 하지만 모델 원본 산출물의 배경 부분에 큰 문제가 있었고 몇몇 개선할 부분이 있었다.

  저자 Mayer는 FlowNet의 구조를 disparity와 scene flow 추정에 차용했다. Ilg는 기본 FlowNet를 여러 겹 쌓아서 FlowNet2라는 거대 모델을 만들었는데, 이는 Sintel benchmark에서 SOTA를 달성하기도 했다. 저자 Ranjan & Black은 SpyNet이라는 소형 공간 pyramid 네트워크를 개발했는데, Sintel benchmark에서 SOTA까지는 아니지만 FlowNetC와 비슷한 성능을 확보했다.

  다음과 같은 비지도 학습 방식의 연구도 진행되었다. Memisevic and Hinton은 이미지의 변형을 탐지하기 위한 비지도학습방법을 제시했고, Long은 CNN 기반의 frame 보간법을 연구했다. Yu는 모델의 loss term에 data constancy term과 spatial smoothness term을 추가한 학습을 연구했다.

✔️ Cost volume

Cost volume은 현재 프레임의 픽셀과 일치하는 다음 프레임의 픽셀을 매칭하는데 필요한 비용을 저장하는 것이다. 해당 비용을 계산하는 것은 optical flow의 특수한 케이스 중 하나로, stereo matching을 위한 일반적인 과정이다. 최근의 연구들은 전체 Cost volume을 한 scale에서 계산하는 방법을 주로 사용하는데, 이러한 방식은 과도한 계산량과 메모리 사용량을 요구한다. 본 논문에서는 여러 pyramid levels를 통해 부분적인 Cost volume을 계산함으로써 효율적인 모델을 개발했다.

✔️ Datasets

  다른 vision task들과 다르게 Optical flow 분야의 ground truth를 갖는 현실 데이터를 얻기는 매우 힘들다. 따라서 이전의 연구들에서는 "Yosemite"와 같은 임의로 만들어낸 데이터를 사용하곤 했는데, 실제 현실 데이터에는 잘 적용되지 못했다.

   KITTI와 Sintel 데이터셋은 Optical flow 분야에서 현재 가장 어렵고 널리 알려져 있다. KITTI는 정적인 데이터와 큰 움직임을 갖거나 심한 조명 변화를 갖는 동적인 데이터를 포함하여 어려운 데이터이며, Sintel은 open source 영화 그래픽 데이터인데 final 버전에서는 강한 기후변화효과와 모션 블러, 카메라 노이즈를 포함하여 어려운 데이터이다. 본 논문에서 제시하는 모델은 위 두 데이터셋에 대해 제시된 다양한 방법론들보다 뛰어난 성능을 확보했다.

✔️ CNN models for dense prediction tasks in vision

Denosing autoencoder(보통 Encoder와 Decoder 사이에 Skip connection과 동반되어 시용되는 구조)는 Computer vision분야에서 dense prediction을 할 때 주로 사용된다. 최근의 연구들에서는 Dilated convolution 레이어가 contextual 정보 활용과 semetic segmentation를 위한 세부사항을 개선하는데 더 낫다는 점이 확인되었다. 

  따라서 본 논문에서 제시하는 모델 또한 optical flow를 위한 contextual 정보 통합과 더 나은 성능 확보를 위해 dilated convolution을 활용한다. 

➡️ Approach

위 Figure3에서는 PWC-Net의 주요 모듈을 위주로 요약한 구조를 보여주며, 본문에서는 전통적인 coarese-to-fine 접근법과 비교한 몇 가지 차이점에 대해서 개괄적으로 설명한다. 이후에는 각 모듈들에 대해 자세히 설명한다.

( 개인적으로, 아래의 내용을 이해하는데 논문의 Figure3 보다 링크의 이미지가 더 직관적이고 편했다. )

1. 원본 이미지는 그림자와 조명의 변화에 따라 변동성이 있으므로 이를 고려할 수 있도록, 고정된 pyramid를 대신해서 학습가능한 feature pyramid로 대체했다
2. 큰 모션을 추정할 수 있도록 하기 위해, 고정된 warping 방식을 사용하는 대신 warping layer를 사용했다
3. 원본 이미지보다 optical flow 정보를 더 잘 드러내는 cost volume을 사용하기 위해 이를 계산하는 CNN layer를 사용했다
4. warping과 cost volume은 학습가능한 파라미터를 사용하지 않음으로써 모델의 사이즈를 줄였다
5. median filtering, bilateral filtering과 같은 전통적인 방식에서 사용한 후처리방식을 대체하기 위해서, context layer를 사용했다

✔️ Feature pyramid extractor

두 입력 이미지 \( \mathbf{I}_1\)과 \( \mathbf{I}_2\)이 주어졌을 때, 각 이미지의 feature 추출을 위해 \(L\) 개의 층을 갖는 pyramid를 사용한다. 이때 pyramid의 가장 최하층값은 원본 입력 이미지와 동일하다. \((i.e., \mathbf{c}_t^0=\mathbf{I}_t)\)

\(l\) 번째 pyramid 층의 feature 표현 \( \mathbf{c}_t^l\)을 만들기 위해서, \(l-1\) 번째 층의 feature 표현 \( \mathbf{c}_t^{l-1}\)을 convolutional filter layers를 통해 크기를 반으로 downsample한다. 첫 번째부터 여섯 번째 층까지의 feature channel 수는 각각 [16, 32, 64, 96, 128, 196]을 사용했다.

✔️ Warping layer

\({l}\)번째 층에서 두 번째 이미지의 feature를 첫 번째 이미지 쪽으로 warping 하게 되는데, 이때 \({l+1}\) 번째 층에서 가져온 optical flow를 2배로 키운 upsampled flow를 사용한다.

${ \mathbf{c}_w^l }( \mathbf{x} )= { \mathbf{c}_2^l}( \mathbf{x} + { \mathbf{up}_2}( \mathbf{w}^{l+1} )( \mathbf{x}) ), \tag{1}$

\(\mathbf{x}\)는 이미지의 픽셀 인덱스이고 \(\mathbf{up}_2(\mathbf{w}^{l+1})\)가 upsampled flow인데, 이는 pyramid의 최고 층에서는 그다음 층이 존재하지 않기 때문에 0으로 설정한다. 그리고 warping 연산과 CNN feature 및 flow 계산을 수행할 때 backpropagation을 가능하게 하기 위해서 bi-linear 보간법을 사용했다. 위와 같은 warping 방식은 물체의 모든 포인트의 움직임이 일정하지 않은 비병진 움직임에서도 기하학적인 왜곡을 보상해 줄 수 있으며, 이미지 패치를 올바른 크기로 설정할 수 있는 효과가 있다.

✔️ Cost volume layer

Cost volume은 현재 프레임의 픽셀과 일치하는 다음 프레임의 픽셀을 서로 매칭하는데 드는 "비용"을 계산한 정보이다. 이때의 "비용"을 본 논문에서는 첫 번째 이미지 feature와 warping 된 두 번째 이미지의 feature 사이의 correlation으로 정의한다. 

$ \mathbf{c v}^l\left(\mathrm{x}_1, \mathrm{x}_2\right)=\frac{1}{N}\left(\mathbf{c}_1^l\left(\mathrm{x}_1\right)\right)^{\top} \mathbf{c}_w^l\left(\mathrm{x}_2\right), \tag{2} $

\({\top}\)는 전치 연산이며, \({N}\)은 column vector \({\mathbf{c}_1^l\left(\mathrm{x}_1\right)}\)의 길이이다. \({L}\) 번째 층 pyramid에서 제한적인 \({d}\) 픽셀 범위로 부분적인 cost volume를 계산하게 된다\(\left({i.e., \left|\mathrm{x}_1-\mathrm{x}_2\right|_{\infty} \leq d}\right) \). 최상층에서 한 픽셀의 움직임은 full resolution 이미지에서 \(2^{L-1}\) 픽셀의 움직임과 동일하기 때문에 \({d}\) 값은 작게 설정한다. 3D cost volume의 차원은 \(d^2 \times{H}^l  \times{W}^l\)인데, \({H}^l\) 과 \({W}^l\)는 각각 \(l\) 번째 pyramid 층의 높이와 너비를 의미한다.

✔️ Optical flow estimator

여러 층의 CNN으로 구성된 Optical flow estimator은 cost volume, 첫 번째 이미지의 feature, upsampled 된 다음 층의 optical flow, 현재 층의 flow \({\mathbf{w}^l}\)를 입력으로 받는다. convolution layer의 채널 수는 모든 pyramid 층에서 동일하게 [128, 128, 96, 64, 32]을 사용한다. 단, 각 층의 estimator들은 parameter는 공유하지 않고 각자의 값을 가지며, \({l}_0\)층에 도달할 때까지 모든 층에서 반복된다. 또한 이 estimator 구조는 DenseNet connection을 함께 사용함으로써 성능을 강화될 수 있는데, 이 경우에는 이전 layer의 입력과 출력값을 현재 layer의 입력값으로 사용하게 된다. 따라서 전통적인 방식보다 더 직접적인 연결을 가짐으로써 이미지 분류 성능을 향상하는데 도움을 준다. 본 논문의 저자는 이 아이디어를 구현하여 테스트했다.

✔️ Context network

전통적인 flow 방법론은 주로 후처리 과정을 통해서 contextual 정보를 사용했다. 이 점에 착안해서 본 논문에서는 context-network를 사용하여, 각 pyramid 층에 맞도록 모델의 인지 범위(receptive filed) 크기를 효율적으로 늘릴 수 있게 구현했다. context-network는 이전 층과 현재 층에서 추정된 flow를 입력으로 받고, refined flow를 출력한다.

Context-network는 feed-forward CNN이며 dilated convolution을 기반으로 고안되었다. 총 7개의 convolution layer로 구성되어 있고, 각 layer는 \(3\times3\)의 spatial 한 kernel을 갖는다. 또한 각 layer들은 서로 다른 dilation 상수 \({k}\)를 갖는데, 이는 입력 unit이 layer 내에서 filter 되는 과정에서 수평 혹은 수직으로 \({k}\) 개만큼 떨어진 unit들만을 고려한다는 의미이다. 이러한 구조는 큰 수의 dialation 상수를 가짐으로써 더욱 넓은 인지 범위를 가지게 되지만 계산량 자체는 크게 늘어나지 않는다는 효과가 있다. 본 논문에서는 최하층부터 최상층까지 [1, 2, 4, 8, 16, 1, 1]의 dilation 상수 값을 사용했다.

✔️ Training loss

Pyramid의 각 층의 pyramid extractor와 optical flow estimator들을 아울러, 모델 전체에서 학습할 수 있는 모든 parameter의 집합을 \({\Theta}\)로 정의한다. (단, warping과 cost volume 계산에는 학습 가능한 parameter가 없음에 주의). 또한 pyramid \({l}\) 층에서 추정한 flow를 \({\mathbf{w}_{\Theta}^l}\)로, 일치하는 supervision signal을 \({\mathbf{w}_{\mathbf{GT}}^l}\)로 표기한다. 본 논문에서는 FlowNet에서 제안된 multi-scale training loss를 사용한다. 

$ \mathcal{L}(\Theta)=\sum_{l=l_0}^L \alpha_l \sum_{\mathrm{x}}\left|\mathbf{w}_{\Theta}^l(\mathrm{x})-\mathbf{w}_{\mathrm{GT}}^l(\mathrm{x})\right|_2+\gamma|\Theta|_2, \tag{3} $

\({|\cdot|}_2\)은 벡터의 \(\mathbf{L}2\)norm을 계산하는 것이고, 두번째 항은 모델의 parameter에 대한 regularization term을 의미한다. Fine-tuning을 위해서는 다음과 같이 robust한 training loss를 사용한다.

$ \mathcal{L}(\Theta)=\sum_{l=l_0}^L \alpha_l \sum_{\mathbf{x}}\left(\left|\mathbf{w}_{\Theta}^l(\mathrm{x})-\mathbf{w}_{\mathbf{G T}}^l(\mathbf{x})\right|+\epsilon\right)^q+\gamma|\Theta|_2 \tag{4} $

\({|\cdot|}\)은 \(\mathbf{L}1\)norm을 계산하는 것이고, \({q < 1}\)의 제약을 통해 outlier에 대해 더 적은 페널티를 부여하는 효과를 준다. (\(\epsilon\)은 아주 작은 상수)

들어가며

🦩 Flamingo는 NeurIPS 2022에 Accept 되었던 Google DeepMind의 논문이다. 간단하게 Pretrained된 Vision 모델과 Language 모델을 연결한 새로운 모델 구조를 제시한 논문이라고 설명할 수 있다. 본 포스트에서는 Paper의 Appendix를 참고하여 Flamingo의 구조를 구성하는 각 모듈에 대한 구체적인 이해를 바탕으로 내용을 리뷰하고자 한다. 따라서 Flamingo의 개괄적인 내용은 생략한다.

(paper link : https://proceedings.neurips.cc/paper_files/paper/2022/hash/960a172bc7fbf0177ccccbb411a7d800-Abstract-Conference.html)

 전체 모델 구조

Vision Encoder

: from pixels to features

Vision Encoder는 이미지와 텍스트가 섞인 입력 데이터 중, 이미지 데이터의 Feature를 추출하는 역할을 수행하는 모듈

• NFNet(Normalizer-Free ResNet)-F6 모델을 pretrain시킨 뒤 freeze 시켜서 Vision Encoder 모듈로 사용
  • 이미지와 텍스트 데이터 쌍들에 대해서 Contrastive objective을 통해 pretrain함
  • (Appendix B.1.3) 내용
    • 저자는 해당 Encoder를 바닥 부터 새롭게 학습시켰다고 함 (trained from scratch)
    • Vision Encoder와 별개로 BERT를 사용한 Language Encoder를 함께 학습시켰는데, Vision과 Language 데이터 쌍은 각 Encoder를 통과하면서 공유되는 embedding space위에 표현됨
      
      • 실제 Flamingo 모델에서는 Vision Encoder의 가중치만 사용하고, Language Encoder는 사용하지 않음
    • 해당 embedding된 값들을 통해 Contrastive learning 수행
      • Multi-class cross-entropy를 사용하여, 같은 쌍에 속하는 두 embedding 값의 유사도는 커지고 다른 쌍에 속하는 두 embedding 값의 유사도는 작아지도록 함
      •  text-to-image constrastive loss 와 image-to-text constrastive loss를 사용해서 두 loss의 합이 최소가 되도록 학습함
• 이미지 데이터의 경우,  2D인 해당 Layer의 최종 산출물을 1D로 Flatten함 (2D → 1D)
• 비디오 데이터의 경우,  초당 1장의 이미지(1 FPS)로 샘플링한 뒤 이미지 처리와 동일한 방식을 각각 수행한다(3D → 1D )
  • 단, 비디오의 시간 순서 정보 손실을 방지하기 위해서 temporal embedding값을 각 프레임 이미지 데이터에 더해준다.  
• 이후 1D Sequence는 다음 모듈인 Perceiver Resampler의 입력으로 사용 

Perceiver Resampler

: from varying-size large feature maps to few visual tokens

Perciever Resampler는 Vision Encoder의 산출물을 frozen 된 language 모델에 맞는 입력 형태로 변환하는 징검다리의 역할을 수행하는 모듈

• Vision Encoder에서 이미지 혹은 비디오 데이터의 feature를 큰 수의 차원에 표현하게 되는데, 이를 고정된 (논문에서는 64) 개수의 이미지 토큰으로 변환
• 위 Figure 5의 예시를 보면, 비디오 데이터의 각 프레임은 Vision Encoder를 통과하여 feature map을 만들게 되고, 이 프레임들의 시간 정보를 유지하기 위해 temporal embedding 값을 더해준 다음 flatten 한 토큰을 learned latent queries와 concat한다. 이를 Perceiver Resample 내의 attention에서 Key와 Value로 사용하게 되고, learned latent queries는 Query가 되어 연산하게 된다.
• 모듈의 출력 토큰의 개수는 Query로 사용된 learned latent queries의 수와 동일함
• 이처럼 큰 수의 차원을 갖는 vision feature map을 고정된 수의 차원을 갖는 vision token으로 resample 함으로써, 이후 cross-attention을 수행할 때 계산 비용 측면에서 이점을 가짐

Gated Cross-Attention Dense layer

시각적인 정보와 언어적인 정보를 통합하여 다음 토큰을 예측할 수 있게 해주는 모듈

• Freeze된 LM을 활용하기 위해서는 Vision feature와 Language feature를 모두 고려한 데이터 표현 방식이 필요함
• Perceiver Resampler에서 생성한 Vision feature(X)을 Key, Value로 사용하고 Language input(Y)을 Query로 하는 Cross-Attention layer을 통해서 시각적 정보와 언어적 정보를 통합함

• Cross-Attention layer에서 Masking 기법을 사용
  
  • Text의 현재 위치 바로 직전에 있었던 Image/Video 만을 고려하도록 Mask를 씌우고 학습함 

https://www.coursera.org/learn/generative-ai-with-llms/lecture/9uWab/course-introduction

들어가며

전 직장 동료가 운영하는 모여서 각자 글쓰기 동아리에 함께 참여하게 되면서, 그동안 미뤄왔던 LLM에 대한 기초 공부를 포스팅으로 남기고자 한다. 총 3주차로 짜여진 코스를 주차 별로 수강하면서 LLM 전반에 대한 흐름을 이해하고 간단한 예제를 직접 구현하는 것이 목표이다. 각 강의의 내용을 정리하고 이해를 돕기위해 영상에 나오는 그림들을 첨부할 예정이다.

➡️ Generative AI & LLMs

• LLM에 입력값으로 전달하는 텍스트를 Prompt라고 함
  • 일반적으로 수천 단어를 입력할 수 있지만, 모델마다 상이함
• LLM의 결과값은 Completion이라고 함
  • 즉, LLM의 inference값
  • 원래 입력한 Prompt 텍스트와 생성된 텍스트를 포함

➡️ LLM use cases and tasks

• 최근 LLM과 Generative AI는 chat bot 개발에 집중됨
• Prompt를 기반으로 에세이를 작성하거나, 텍스트를 요약하거나, 서로 다른 두 언어간의 번역 작업을 수행할 수 있음
• 자연어를 기계 코드로 번역할 수 있음
• 뉴스 기사를 입력하여 모든 사람과 장소를 식별하는 작업을 할 수 있음 (NER: Named Entity Recognition)
• 외부 데이터 소스와 연동해서 LLM을 강화하는 작업을 할 수 있음
  • Pretrain하는 과정에서 알지 못하는 정보를 모델에 제공하여 추가로 학습시키는 과정

➡️Text generation before transformers

• 생성 알고리즘은 새로운 기술이 아님
  • 기존 RNN은 당시에 잘 수행되었지만, 부족한 계산 자원과 많은 메모리 사용으로 인해 제한적이었음
  • RNN의 단점을 해결한 Transformer 아키텍쳐의 등장으로 오늘날의 Generative AI 발전이 가능했음
    • GPU를 사용할 수 있도록 효율적인 확장이 가능함
    • 입력 데이터를 병렬처리하여 더 큰 학습데이터를 활용할 수 있음 

➡️Transformers architecture

Transformer 아키텍처의 RNN과 다른 특징들을 통해 언어 모델 성능이 크게 향상되었음

• 문장 내에서 단어와 인접한 단어들 뿐만 아니라 다른 모든 단어와의 관련성을 학습함 (Self-Attention, 향후 강의에서 자세히 다룸)

Transformer 구조는 Encoder와 Decoder로 분리할 수 있으며, 서로 연동되어 작동하고 여러 유사점을 가짐

텍스트를 Transformer에 Inputs으로 전달하기 위해서는 토큰화가 선행되어야 함

• 토큰화는 단어 문자열을 모델의 Input으로 사용하기 위해 숫자(Token IDs)로 변환하는 방법
• 토큰화를 통해 얻는 숫자(Token IDs)는 모델이 받아드릴 수 있는 모든 단어의 사전 내 위치를 나타냄
• 모델을 학습시킬 때와 추론(텍스트 생성)할 때 사용하는 토큰화 방식이 같아야 함

변환된 각 토큰은 Embedding 레이어에 전달됨

• Embedding 레이어는 학습 가능한 벡터 임베딩 공간
• 숫자로 표현된 토큰은 Embedding 레이어를 통과함으로써 다차원 벡터로 변환됨 
• 다차원 벡터로 Embedding하는 과정을 통해 단어 토큰의 의미와 문맥을 학습함

• 위 예를 보면, 각 단어 토큰들이 512크기의 벡터로 Embedding 되었음을 볼 수 있음
  • 512는 Transformer 원본 논문에서 제시한 Embedding 벡터 크기이고, 상황에 따라 조절해서 사용할 수 있음

Embedding된 다차원 토큰 벡터가 Encoder 및 Decoder의 Input으로 사용되기 전에 마지막으로 Positional Encoding 과정을 거치게 됨

• 모델의 Input은 병렬적으로 처리되기 때문에, 문장에서의 단어 순서 정보가 누락되게 됨
• Positional Encoding을 통해 단어 순서의 정보를 더해줌으로써 단어 위치의 관계성을 잃지 않게 됨

토큰 벡터와 Positional Encoding 벡터를 합산한 벡터는 Encoder 및 Decoder에 전달되어 Self-Attention 레이어로 전달됨

• 모델 학습 중 학습되는 Attention Weight는 해당 입력 문장 내에서 각 단어가 다른 모든 단어에 미치는 중요도를 대변함

Self-Attention을 통해서 모델은 문장 내 각 단어의 문맥적 종속성을 잘 포착할 수 있지만, 이러한 일련의 과정을 여러 다른 주체가 수행하도록 하는 방법이 Multi-headed Self-Attention임

• Multi-headed Self-Attention은 여러 세트(head)의 Self-Attention 과정을 서로 독립적으로 병렬적으로 학습하는 방법
• 여러 head에서 입력 문장을 각기 다른 각도에서 바라보며 학습을 진행한다고 해석할 수 있음
  • 각 head의 Attention weight는 무작위로 초기화 되고 충분한 Train데이터와 시간이 주어져 입력 문장에 대한 다양한 측면을 학습하는 것
• head의 수는 모델마다 상이하지만 12~100개가 일반적

모든 head의 Attention weight가 계산 되고 나면, Fead forward 레이어를 통해서 모든 토큰의 Logit 벡터를 얻을 수 있음

이후에 Logit벡터를 Softmax 레이어를 통과시켜 문장 내의 모든 단어에 대한 확률값을 구할 수 있음

• Softmax 출력값에는 입력 문장에 있는 모든 단어에 대한 확률이 포함됨
• 가장 높은 확률을 갖는 단어가 모델이 예측하는 단어가 됨
• Task에 따라서 이 최종 벡터를 활용하는 방법이 다양할 수 있음

➡️Generating text with transformers

이전 lecture에서 Transformer의 아키텍처 주요 구성 요소들에 대해 개요를 소개했고, 이번 lecture에서는 전체 프로세스에 대한 설명을 진행

Example) 프랑스어를 영어로 번역하는 Transformer

1. Transformer를 학습시킬 때 사용한 토큰화 방식을 사용해서 입력 문장(프랑스어)의 단어들을 토큰화
2. 토큰들은 Embedding 레이어를 통과하여 다차원 벡터로 변환됨
3. 변환된 벡터는 Encoder의 Multi-headed Self-Attention 레이어와 Feed forward 네트워크를 통과하여 출력됨
   1. 이때의 Encoder 출력값은 입력 문장의 구조와 의미를 심층적으로 표현함
4. Encoder의 출력값은 Decoder의 중간에 삽입되어 Decoder의 Self-Attention의 일부 입력값으로 사용됨
5. 문장의 시작을 알리는 토큰이 Decoder의 입력에 추가됨
6. 이 상태가 되면 Decoder가 다음 토큰을 예측하도록 트리거되고, Encoder의 출력값을 바탕으로 다음 토큰을 예측함
   1. Decoder의 Self-Attention 출력은 Feed forward 네트워크와 Softmax를 거쳐서 첫 번째 토큰을 예측하게 됨
7. 모델이 문장 종료를 알리는 토큰을 예측할 때 까지 Decoder의 출력 토큰을 Decoder의 입력 토큰으로 다시 전달하여 다음 토큰 예측을 트리거하며 이 루프를 계속함
8. 이 시점에서 최종 예측된 토큰들을 해독해서 다시 단어로 변환하여 최종 출력을 생성함

위의 번역 예제에서는 Encoder와 Decoder를 모두 사용했지만, Encoder만을 사용하는 등의 아키텍처 변형을 할 수 있음

• Encoder만을 사용하는 모델
  • 입력 시퀀스와 출력 시퀀스의 길이가 같지 않도록하는 레이어를 추가함으로써 감정 분석이나 분류 문제를 풀 수 있음
  • e.g. BERT
• Encoder와 Decoder를 모두 사용하는 모델
  • 번역 문제와 같이 시퀀스 간 작업에서 잘 작동함
  • e.g. BART, T5
• Decoder만을 사용하는 모델
  • 오늘날 가장 일반적으로 사용됨
  • e.g. GPT, BLOOM, Jurassic, Lama